brmm

Module: missions.nodes.classification.svm_variants.brmm

Relative Margin Machines (original and some variants)

Inheritance diagram for pySPACE.missions.nodes.classification.svm_variants.brmm:

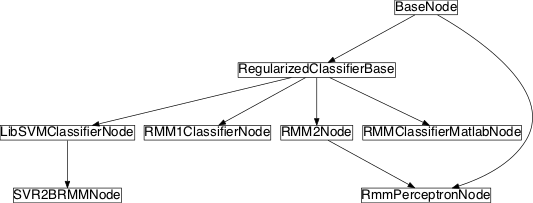
Class Summary

RMM2Node([random, omega, max_iterations, ...])	Classify with 2-norm SVM relaxation (b in target function) for BRMM
RMM1ClassifierNode([normalize_C, ...])	Classify with 1-Norm SVM and relative margin
SVR2BRMMNode([range, complexity])	Simple wrapper around epsilon-SVR with BRMM parameter mapping
RMMClassifierMatlabNode([range])	Classify with Relative Margin Machine using original matlab code
RmmPerceptronNode([version, kernel_type, ...])	Online Learning variants of the 2-norm RMM

Classes

RMM2Node

class pySPACE.missions.nodes.classification.svm_variants.brmm.RMM2Node(random=False, omega=1.0, max_iterations=inf, version='samples', reduce_non_zeros=True, linear_weighting=False, calc_looCV=False, range_=inf, outer_complexity=None, offset_factor=1, squared_loss=False, co_adaptive=False, co_adaptive_index=inf, history_index=1, **kwargs)

Bases: pySPACE.missions.nodes.classification.base.RegularizedClassifierBase

Classify with 2-norm SVM relaxation (b in target function) for BRMM

The balanced relative margin machine (BRMM) is a modification of the original relative margin machine (RMM). The details to this algorithm can be found in the given reference.

This node extends a successive over relaxation algorithm for adaption on new data with some variants.

For further details, have a look at the given reference, the reduced_descent method which is an elemental processing step and the _inc_train method, which uses the status of the algorithm as a warm start.

References

main
author	Krell, M. M. and Feess, D. and Straube, S.
title	Balanced Relative Margin Machine - The Missing Piece Between FDA and SVM Classification
journal	Pattern Recognition Letters
publisher	Elsevier
doi	10.1016/j.patrec.2013.09.018
year	2014

Parameters

Most parameters are already included into the RegularizedClassifierBase.

random:

Numerical recipes suggests to randomize the order of alpha. M&M suggest to sort the alpha by their magnitude.

(optional, default: False)

omega:

Descent factor of optimization algorithm. Should be between 0 and 2! Numerical recipes uses 1.3 and M&M choose 1.0.

(optional, default: 1.0)

version:

Using the matrix with the scalar products or using only the samples and track changes in w and b for fast calculations. Both versions give totally the same result but they are available for comparison. Samples is mostly a bit faster. For kernel usage only matrix is possible.

(optional, default: “samples”)

reduce_non_zeros:  

In the inner loops, indices are rejected, if they loose there support.

(optional, default: True)

linear_weighting:  

Add a linear weighting in the loss term. We use the index as weight and normalize it to have a total sum of 1.

(optional, default: False)

calc_looCV:

Calculate the leave-one-out metrics on the training data

(optional, default: False)

range_:

Upper bound for the prediction value before its ‘outer loss’ is punished with outer_complexity.

Using this parameter (with value >1) activates the RMM.

(optional, default: numpy.inf)

outer_complexity:  

Cost factor for to high values in classification. (see range_)

(optional, default: `complexity`)

offset_factor:

Reciprocal weight, for offset treatment in the model

0:Use no offset 1:Normal affine approach from augmented feature vectors high:Only small punishment of offset, enabling larger offsets (danger of numerical instability)

If 0 is used, the offset b is set to zero, otherwise it is used via augmented feature vectors with different augmentation factors. The augmentation value corresponds to 1/offset_factor, where 1/0 corresponds to infinity.

(optional, default: 1)

squared_loss:

Use L2 loss (optional) instead of L1 loss (default).

(optional, default: False)

In the implementation we do not use alpha but dual_solution for the variables of the dual optimization problem, which is optimized with this algorithm.

In the RMM case dual solution weights are concatenated. The RMM algorithm was constructed in the same way as in the mentioned references.

As a stopping criterion we use the maximum change to be less than some tolerance.

Exemplary Call

-
    node : 2RMM
    parameters :
        complexity : 1.0
        weight : [1,3]
        debug : True
        store : True
        class_labels : ['Standard', 'Target']

Input:

FeatureVector

Output:

PredictionVector

Author:

Mario Michael Krell (mario.krell@dfki.de)

Created:

2012/06/27

POSSIBLE NODE NAMES:  

• RMM2
• 2RMM
• RMM2Node

POSSIBLE INPUT TYPES:  

• FeatureVector

Class Components Summary

__hyperparameters
_execute(x)	Executes the classifier on the given data vector in the linear case
_inc_train(data, label)	Warm Start Implementation by Mario Michael Krell
_stop_training([debug])	Train the SVM with the SOR algorithm on the collected training data
append_sample(sample)
append_weights_and_class_factors(label)	Mapping between labels and weights/class factors
calculate_weigts_and_class_factors()	Calculate weights in the loss term and map label to -1 and 1
input_types
iteration_loop(M[, reduced_indices])	The algorithm is calling the reduced_descent method in loops over alpha
looCV()	Calculate leave one out metrics
project(value, index)	Projection method of soft_relax
reduce_dual_weight(index)	Change weight at index to zero
reduced_descent(current_dual, M, ...)	Basic iteration step over a set of indices, possibly subset of all
reiterate(parameters)	Change the parameters in the model and reiterate
total_descent(current_dual, M[, reduced_indices])	Different sorting of indices and iteration over all indices
update_classification_function(delta, index)	update classification function parameter w and b
update_data()	Recalculate w, samples and M

__init__(random=False, omega=1.0, max_iterations=inf, version='samples', reduce_non_zeros=True, linear_weighting=False, calc_looCV=False, range_=inf, outer_complexity=None, offset_factor=1, squared_loss=False, co_adaptive=False, co_adaptive_index=inf, history_index=1, **kwargs)

_execute(x)

Executes the classifier on the given data vector in the linear case

prediction value = <w,data>+b

_stop_training(debug=False)

Train the SVM with the SOR algorithm on the collected training data

looCV()

Calculate leave one out metrics

reduce_dual_weight(index)

Change weight at index to zero

calculate_weigts_and_class_factors()

Calculate weights in the loss term and map label to -1 and 1

append_weights_and_class_factors(label)

Mapping between labels and weights/class factors

The values are added to the corresponding list. This is done in a separate function, since it is also needed for adaption.

iteration_loop(M, reduced_indices=[])

The algorithm is calling the reduced_descent method in loops over alpha

In the first step it uses a complete loop over all components of alpha and in the second inner loop only the non zero alpha are observed till come convergence criterion is reached.

reduced_indices will be skipped in observation.

reduced_descent(current_dual, M, relevant_indices)

Basic iteration step over a set of indices, possibly subset of all

The main principle is to make a descent step with just one index, while fixing the other dual_solutions.

The main formula comes from M&M:

Here we use c for the weights for each sample in the loss term, which is normally complexity times corresponding class weight. y is used for the labels, which have to be 1 or -1.

In the sample version only the diagonal of M is used. The sum with the alpha is tracked by using the classification vector w and the offset b.

update_classification_function(delta, index)

update classification function parameter w and b

project(value, index)

Projection method of soft_relax

total_descent(current_dual, M, reduced_indices=[])

Different sorting of indices and iteration over all indices

_inc_train(data, label)

Warm Start Implementation by Mario Michael Krell

The saved status of the algorithm, including the Matrix M, is used as a starting point for the iteration. Only the problem has to be lifted up one dimension.

reiterate(parameters)

Change the parameters in the model and reiterate

append_sample(sample)

update_data()

Recalculate w, samples and M

__hyperparameters = set([ChoiceParameter<kernel_type>, NoOptimizationParameter<linear_weighting>, BooleanParameter<squared_loss>, NoOptimizationParameter<dtype>, NoOptimizationParameter<use_list>, NoOptimizationParameter<kwargs_warning>, BooleanParameter<regression>, QLogUniformParameter<max_iterations>, NormalParameter<ratio>, NoOptimizationParameter<output_dim>, LogNormalParameter<tolerance>, UniformParameter<nu>, NoOptimizationParameter<store>, NoOptimizationParameter<input_dim>, LogNormalParameter<epsilon>, NoOptimizationParameter<retrain>, ChoiceParameter<offset_factor>, QNormalParameter<offset>, NoOptimizationParameter<omega>, LogUniformParameter<complexity>, QUniformParameter<max_time>, NoOptimizationParameter<debug>, LogUniformParameter<range_>, NoOptimizationParameter<keep_vectors>])

input_types = ['FeatureVector']

RMM1ClassifierNode

class pySPACE.missions.nodes.classification.svm_variants.brmm.RMM1ClassifierNode(normalize_C=False, outer_complexity=None, range=2, **kwargs)

Bases: pySPACE.missions.nodes.classification.base.RegularizedClassifierBase

Classify with 1-Norm SVM and relative margin

Implementation via Simplex Algorithms for exact solutions.

It is important, that the data is reduced and has not more then 2000 features.

This algorithm is an extension of the original RMM as outlined in the reference.

References

main
author	Krell, M. M. and Feess, D. and Straube, S.
title	Balanced Relative Margin Machine - The Missing Piece Between FDA and SVM Classification
journal	Pattern Recognition Letters
publisher	Elsevier
doi	10.1016/j.patrec.2013.09.018
year	2013

Parameters

complexity:

Complexity sets the weighting of punishment for misclassification in comparison to generalizing classification from the data. Value in the range form 0 to infinity.

(optional, default: 1)

outer_complexity:  

Outer complexity sets the weighting of punishment being outside the range in comparison to generalizing classification from the data and the misclassification above. Value in the range form 0 to infinity. By default it uses the outer complexity. For using infinity, use numpy.inf, a string containing inf or a negative value.

(recommended, default: complexity_value)

weight:

Defines parameter for class weights. I is an array with two entries. Set the parameter C of class i to weight*C.

(optional, default: [1,1])

range:

Defines constraint radius for the outer boarder of the classification. Going to infinity, this classifier will be identical to the 1 Norm SVM. This parameter should be always greater then one. Going to one, the classifier will be a variant of the Regularized Linear Discriminant analysis.

(optional, default: 2)

class_labels:

Sets the labels of the classes. This can be done automatically, but setting it will be better, if you want to have similar predictions values for classifiers trained on different sets. Otherwise this variable is built up by occurrence of labels. Furthermore the important class (ir_class) should get the second position in the list, such that it gets higher prediction values by the classifier.

(recommended, default: [])

debug:

If debug is True one gets additional output concerning the classification.

(optional, default: False)

store:

Parameter of super-class. If store is True, the classification vector is stored as a feature vector.

(optional, default: False)

Exemplary Call

-
    node : 1RMM
    parameters :
        complexity : 1.0
        weight : [1,2.5]
        debug : False
        store : True
        range : 2

Input:

FeatureVector

Output:

PredictionVector

Author:

Mario Krell (Mario.krell@dfki.de)

Revised:

2010/04/09

POSSIBLE NODE NAMES:  

• 1RMM
• RMM1ClassifierNode
• RMM1Classifier

POSSIBLE INPUT TYPES:  

• FeatureVector

Class Components Summary

__hyperparameters
_stop_training([debug])	Finish the training, i.e.
calculate_classification_vector(model)	Copy from Norm1ClassifierNode due to avoid cross importing
calculate_slack_variables(model)	Calculate slack variables from the given SVM model
create_problem_matrix(n, e)
get_solution_with_timeout(c, n, e, h)
input_types

__init__(normalize_C=False, outer_complexity=None, range=2, **kwargs)

create_problem_matrix(n, e)

_stop_training(debug=False)

Finish the training, i.e. train the SVM.

This makes the same as the 1-Norm RMM, except that there are additional restrictions pushing the classification into two closed intervals instead of two open. At both ends there is the same kind of soft Margin.

get_solution_with_timeout(c, n, e, h)

calculate_slack_variables(model)

Calculate slack variables from the given SVM model

calculate_classification_vector(model)

Copy from Norm1ClassifierNode due to avoid cross importing

__hyperparameters = set([ChoiceParameter<kernel_type>, NormalParameter<ratio>, NoOptimizationParameter<kwargs_warning>, NoOptimizationParameter<dtype>, NoOptimizationParameter<output_dim>, NoOptimizationParameter<use_list>, LogUniformParameter<complexity>, LogNormalParameter<epsilon>, BooleanParameter<regression>, NoOptimizationParameter<retrain>, QNormalParameter<range>, NoOptimizationParameter<store>, NoOptimizationParameter<input_dim>, QNormalParameter<offset>, NoOptimizationParameter<debug>, QUniformParameter<max_time>, BooleanParameter<normalize_C>, LogNormalParameter<tolerance>, UniformParameter<nu>, NoOptimizationParameter<keep_vectors>])

input_types = ['FeatureVector']

SVR2BRMMNode

class pySPACE.missions.nodes.classification.svm_variants.brmm.SVR2BRMMNode(range=3, complexity=1, **kwargs)

Bases: pySPACE.missions.nodes.classification.svm_variants.external.LibSVMClassifierNode

Simple wrapper around epsilon-SVR with BRMM parameter mapping

POSSIBLE NODE NAMES:  

• SVR2BRMMNode
• SVR2BRMM

POSSIBLE INPUT TYPES:  

• FeatureVector

Class Components Summary

input_types

__init__(range=3, complexity=1, **kwargs)

input_types = ['FeatureVector']

RMMClassifierMatlabNode

class pySPACE.missions.nodes.classification.svm_variants.brmm.RMMClassifierMatlabNode(range=2, **kwargs)

Bases: pySPACE.missions.nodes.classification.base.RegularizedClassifierBase

Classify with Relative Margin Machine using original matlab code

This node integrates of the “original” Shivaswamy RMM code. This RMM is implemented in Matlab and uses the mosek optimization suite.

For this node to work, make sure that

1. Matlab is installed.
2. The pymatlab Python package is installed properly. pymatlab can be downloaded from http://pypi.python.org/pypi/pymatlab/0.1.3 For a MacOS setup guide please see https://svn.hb.dfki.de/IMMI-Trac/wiki/pymatlab
3. mosek is installed and matlab can access it. See http://mosek.com/ People with university affiliation can request free academic licenses within seconds from http://license.mosek.com/cgi-bin/student.py

References

main
author	Shivaswamy, P. K. and Jebara, T.
title	Maximum relative margin and data-dependent regularization
journal	Journal of Machine Learning Research
pages	747-788
volume	11
year	2010

Parameters

complexity:

Complexity sets the weighting of punishment for misclassification in comparison to generalizing classification from the data. Value in the range form 0 to infinity.

(optional, default: 1)

range:

Defines constraint radius for the outer boarder of the classification. Going to infinity, this classifier will be identical to the SVM. This parameter should be always greater then one. Going to one, the classifier will be a variant of the Regularized Linear Discriminant analysis.

(optional, default: 2)

Note

This classification node doesn’t have nice debugging outputs as most errors will occur in mosek, i.e., from within the matlab session. In the rmm.m matlab code one might want to save the ‘res’ variable as it contains mosek error codes.

Note

This implementation doesn’t use class weights, i.e., w=[1,1] is fixed.

Exemplary Call

-
    node :  RMMmatlab
    parameters :
        complexity : 1.0
        range : 2.0
        class_labels : ['Standard', 'Target']

Input:

FeatureVector

Output:

PredictionVector

Author:

David Feess (David.Feess@dfki.de)

Revised:

2011/03/10

POSSIBLE NODE NAMES:  

• RMMClassifierMatlabNode
• RMMClassifierMatlab
• RMMmatlab

POSSIBLE INPUT TYPES:  

• FeatureVector

Class Components Summary

__hyperparameters
_stop_training([debug])	Finish the training, i.e.
input_types

__init__(range=2, **kwargs)

_stop_training(debug=False)

Finish the training, i.e. train the RMM. Essentially, the data is passed to matlab, and the classification vector w and the offset b are returned.

__hyperparameters = set([ChoiceParameter<kernel_type>, NormalParameter<ratio>, NoOptimizationParameter<input_dim>, NoOptimizationParameter<dtype>, NoOptimizationParameter<output_dim>, QNormalParameter<offset>, NoOptimizationParameter<use_list>, UniformParameter<nu>, NoOptimizationParameter<retrain>, LogUniformParameter<complexity>, NoOptimizationParameter<keep_vectors>, NoOptimizationParameter<kwargs_warning>, LogNormalParameter<epsilon>, NoOptimizationParameter<debug>, QUniformParameter<max_time>, QNormalParameter<range_>, LogNormalParameter<tolerance>, BooleanParameter<regression>, NoOptimizationParameter<store>])

input_types = ['FeatureVector']

RmmPerceptronNode

class pySPACE.missions.nodes.classification.svm_variants.brmm.RmmPerceptronNode(version='samples', kernel_type='LINEAR', co_adaptive=False, co_adaptive_index=inf, history_index=1, **kwargs)

Bases: pySPACE.missions.nodes.classification.svm_variants.brmm.RMM2Node, pySPACE.missions.nodes.base_node.BaseNode

Online Learning variants of the 2-norm RMM

Parameters

See also

RMM2Node

co_adaptive:

Integrate backtransformation into classifier to catch changing preprocessing

(optional, default: False)

co_adaptive_index:  

Number of nodes to go back

(optional, default: numpy.inf)

history_index:

Number of history index of original data used for co-adaptation

(optional, default: 1)

Exemplary Call

-   node : RmmPerceptronNode
    parameters :
        range : 3
        complexity : 1.0
        weight : [1,3]
        class_labels : ['Standard', 'Target']

Author:

Mario Michael Krell

Created:

2014/01/02

POSSIBLE NODE NAMES:  

• RmmPerceptron
• RmmPerceptronNode

POSSIBLE INPUT TYPES:  

• FeatureVector

Class Components Summary

__hyperparameters
_inc_train(data, label)	Incremental training and normal training are the same
_stop_training([debug])	Do nothing than suppressing mother method
_train(data, class_label)	Main method for incremental and normal training
train(data, label)	Prevent RegularizedClassifierBase method from being called
update_from_history()	Update w from historic data to catch changing preprocessing

__init__(version='samples', kernel_type='LINEAR', co_adaptive=False, co_adaptive_index=inf, history_index=1, **kwargs)

_train(data, class_label)

Main method for incremental and normal training

Code is a shortened version from the batch algorithm.

update_from_history()

Update w from historic data to catch changing preprocessing

__hyperparameters = set([NoOptimizationParameter<kernel_type>, NoOptimizationParameter<linear_weighting>, BooleanParameter<squared_loss>, NoOptimizationParameter<dtype>, NoOptimizationParameter<use_list>, NoOptimizationParameter<kwargs_warning>, BooleanParameter<regression>, QLogUniformParameter<max_iterations>, NormalParameter<ratio>, NoOptimizationParameter<output_dim>, NoOptimizationParameter<version>, LogNormalParameter<tolerance>, UniformParameter<nu>, NoOptimizationParameter<store>, NoOptimizationParameter<input_dim>, LogNormalParameter<epsilon>, NoOptimizationParameter<retrain>, ChoiceParameter<offset_factor>, QNormalParameter<offset>, NoOptimizationParameter<omega>, LogUniformParameter<complexity>, QUniformParameter<max_time>, NoOptimizationParameter<debug>, LogUniformParameter<range_>, NoOptimizationParameter<keep_vectors>])

train(data, label)

Prevent RegularizedClassifierBase method from being called

_inc_train(data, label)

Incremental training and normal training are the same

_stop_training(debug=False)

Do nothing than suppressing mother method